芝诺二分悖论与无穷大是否可被超越？

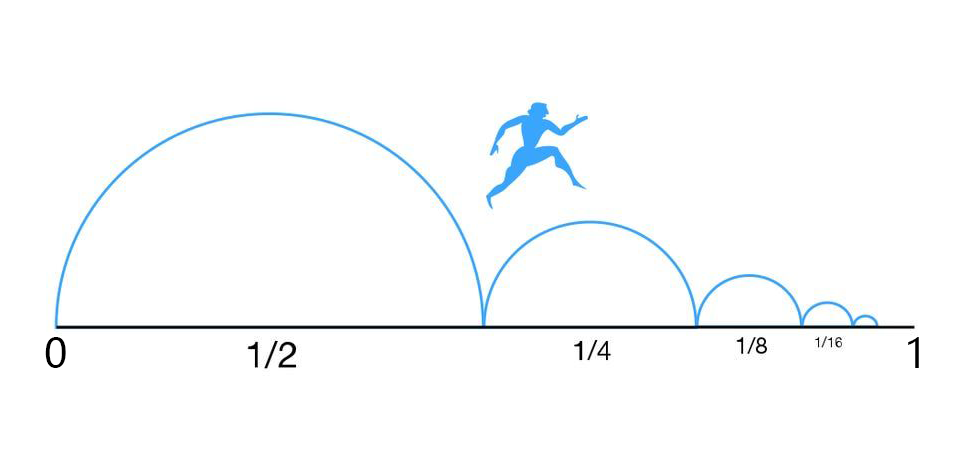
假如说有一个人要从0这个点走到1这个点，显然他首先需要走完这段距离的一半，然后再走完剩余距离的一半，不断按照这种分法分下去前方就有无穷多的分段要走，他怎么可能走得完这无穷多的分段呢？所以他永远无法从0这个点走到1。

^[1] 为了进一步准确表达这个问题的本质，描述里的“这个人”或“他”都可以换成几何上的“一个点”来理解，下文同理，因此这个问题可以理论化表述为：假设一个点要从数轴上的0这个点走到1这个点，显然它首先需要走完这段距离的一半，然后再走完剩余距离的一半，不断按照这种分法分下去前方就有无穷多的分段要走，它怎么可能走得完这无穷多的分段呢？所以这个点永远无法从0这个点走到1。

然而在现实生活中却不是这样的，比如说如果这段距离的长度是1km，即1000米，这个人如果以一米每秒的速度在前进，那么1000秒后也就是16分钟40秒之后他就会走完这1km的路程，并不会永远走不完、永远无法到达。但是按照前面的那种走法总有无穷多分段在前，看起来就是永远走不完，所以无法到达，然而实际上却又可以到达，那么这种说法究竟是错在哪里呢？这就是著名的芝诺二分悖论（Zeno's dichotomy paradox） ^[2] ， 是一个非常有意思有价值的问题，如果你对这个问题感兴趣的话我建议你暂时离开本文回去想几天再回来看如下我跨越了十年的思考认识，因为这会更有收获，这期间虽然断断续续但总的来说通过长时间的思考和逐渐认识，我目前算是对这个问题有了更深入的理解，故此就和大家分享一下我的认识。

首先要说明的是这个悖论涉及到把一条线段“无限分割（infinite divisibility）”，有些物理理论认为是不可能无限二分下去的，因此这个悖论不成立，也就无需探讨，但是本文是要从数学理论的角度探讨这个问题，而无限分割在数学上是成立的，所以下面将从数学的角度解决上面的困惑与好奇。

按照上面的约定将0~1之间的剩余距离进行无限二等分之后再按照走完一半再走剩余的一半的走法走下去，在不确定他能否到达的情况下我们可以确定的是两点：（1）他走过的路程只能是小于或等于1；（2）在他未到达1这个点前他会持续不断地走过一个又一个分段，任何指定的分段都会被逐渐超过。具体我们可以看处于0到1这段距离内的任何一点，尤其是处于前方剩余路程内的任何一点，比如说红色这一点，按照走完一半再走剩余的一半不断走下去的走法它是会被超越的，然后再来看黄色这一点，也是同样可以被超越的，接下来的绿色这一点也是同样可以被超越。

按照这个示例来看任何在0到1内的点或任何小于1的长度都会被走过或超越，所以这个人走过的距离不可能小于1，还记得我们上面确定的“他走过的路程只能是小于或等于1”吗？现在小于1这种可能性已经被排除了，所以他在0~1之间按照走完一半再走剩余的一半的走法永不停歇地走下去最终走过的距离是1，所以他是可以走到终点的。
可奇怪的是我们上面为什么会得出他永远走不到终点的结论呢？让我们返回去逐字逐句地检视一下看看问题出在哪里。看来看去，最终问题只能出现在“他怎么可能走得完这无穷多的分段呢？”这一句上，首先按照上面的规定将剩余路程无限二分的方法确实是可以产生无限多的分段，但是如果执意认为这无限多的分段是走不完的，那么我们就会得出“他永远无法从0这个点走到1这个点”的结论，但实际上即便通过理论分析我们前面也可以得出他是可以走到终点的，因此我们不得不推翻这种直观认识转而去承认“无穷多的数目是可超越的、可跨越的”——这是一个匪夷所思、完全颠覆我们想象的结论。即便是抛开我上面的分析，我们从“他是可以到达终点的”这个实际结果反推回去也不得不承认当他到达终点的那一刻就意味着他已经跨越了无限二分所产生的那无限多的分段，所以“无穷大的数目是可超越的、可跨越的”。从更广义的角度来看，如果一个运动的点从数轴上的0走到1，那么当它到达1的时候无形中也就跨越了0~1之间的无数多个点，这又再一次说明了“无穷大的数目是可超越的、可跨越的”。我们凭直觉认为无穷大的数目是数不完也无法超越的，但是通过芝诺二分悖论我们认识到这种直觉认识是错的。此外，值得进一步思考的另外一个问题是：既然无穷是可以被超越的，那么无穷之后又是怎样一番景象呢？这是更令人神往的境地！

前面的内容是针对普罗大众的讲法，如果能明白其中的思想精髓那也是很有收获的。下面将分别针对具有高一和大一数学基础的读者用数学公式更准确地阐明。

1. 如上所述在不知道他能否到达的情况下我们首先可以确定的是他走过的路程S只能是小于或等于1，即 $S \leq 1$ ；

2. 由于他是不断向前走的，所以可以确定他走过的路程S必然不会小于按上述走法走出来的任何前n个分段的路程之和 $S_{n} = \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \cdots + {(\frac{1}{2})}^{n} = 1 - {(\frac{1}{2})}^{n}$ ，即 $S \geq S_{n}$ ；

3. 另一方面按照上述走法n是不断变大的，可以变得要多大就有多大的，这会使得 $S_{n} = 1 - \left( \frac{1}{2} \right)^{n}$ 可以变得比任何预先给定大于0且小于1的数L都大（只要取 $n>-\log _2(1-L)$ 即可），又因为 $S \geq S_{n}$ ，因此可以最终排除S小于1的可能性，S只能等于1，所以他是可以走到终点的。

我们前面说过这个人要跨过无限多分段才能到达，此处的数学解释里“无限多段”由第三步分析里的“n可以变得要多大就有多大”来体现，更具体地讲n必须从小到大取遍所有正整数（否则这个人便不可能到达），而正整数的个数我们都知道是无限多的。

有大一数学基础的读者可能早已想到公式

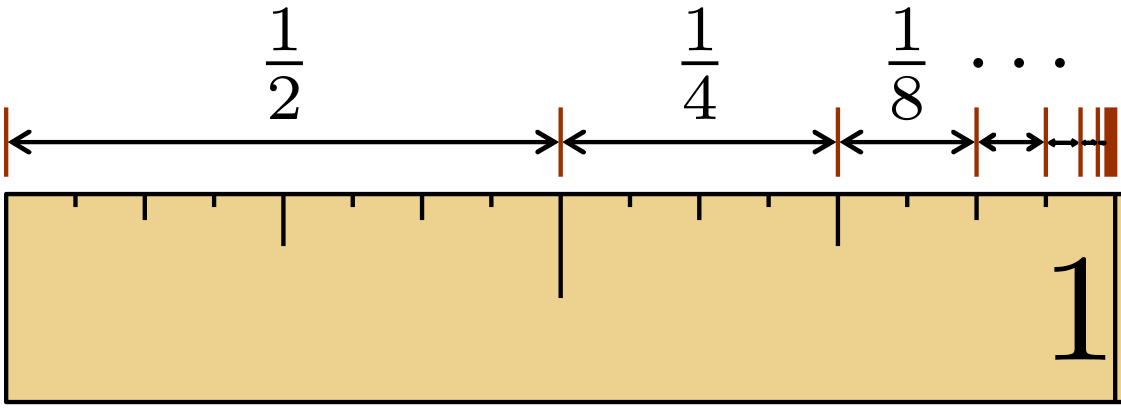
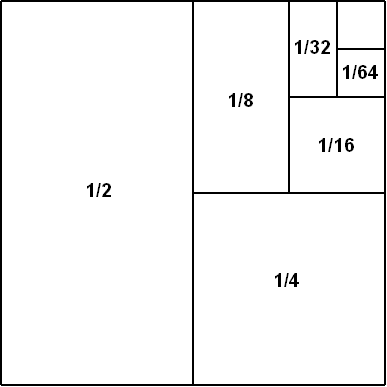
这个公式强有力地说明了他走过的分段长度之和就是1，因此他是可以走到终点的，进而戳穿了芝诺二分悖论，但是如果你搞不清楚 $\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \cdots$ 究竟是无限趋近于1呢还是真真实实准准确确地等于1？那么这个公式仍然无法真正帮助你戳穿芝诺二分悖论。这个无穷级数对应的前n项和 $S_{n} = \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \cdots + {(\frac{1}{2})}^{n} = 1 - {(\frac{1}{2})}^{n}$ 在n变得越来越大的时候如上所述是可以变得比任何预先给定大于0且小于1的数都大的，而另一方面级数 $\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \cdots$ 是不会超过1的，这可以简单地从下图长度为1的线段里的分段长度之和或边长为1的正方形里的小矩形面积之和方面来理解

^[3] ，

^[3:1]
也可以根据定理“ 如果 $\lim _{n \rightarrow \infty} a_n=a$ 并且 $a_n<\beta$ ，那么 $a\leq\beta$ ” ^[4] 得出，即：因为 $\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \cdots = \lim_{n \rightarrow \infty}{S_n} = S$ 且 $S_n=1 - \left( \frac{1}{2} \right)^{n}<1$ ，则有 $S\leq 1$ 。

现在我们综合来看：级数 $\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \cdots$ 一方面比任何大于0且小于1的数都大，另外一方面不会超过1，所以其值最终只能是1，而该级数等同于这个人走过的路程之和，所以公式计算也表明他是可以从0这个点走到1的。同样地，我们前面说过这个人要跨过无限多段分段才能到达，此处的数学解释里“无限多段”由“这个级数的项数是无限多个”来体现，只有这无限多的项数加起来和才是1。
对于这么一个存在超过2500年的经典悖论，本文提供了用和不用公式的两种解答方式，最基本地，读者只要明白第一种讲解方式尤其是里面提到的“无穷大是可以被超越的”就算是掌握到了很有价值的思想。