【视频讲座】用极限或定积分求出来的面积是准确值还是近似值？

The calculus method for calculating the curvilinear area is to divide the shape into many narrow rectangles, sum their areas, and then take the limit of the sum to be the value of the area as the rectangles become narrower and narrower.

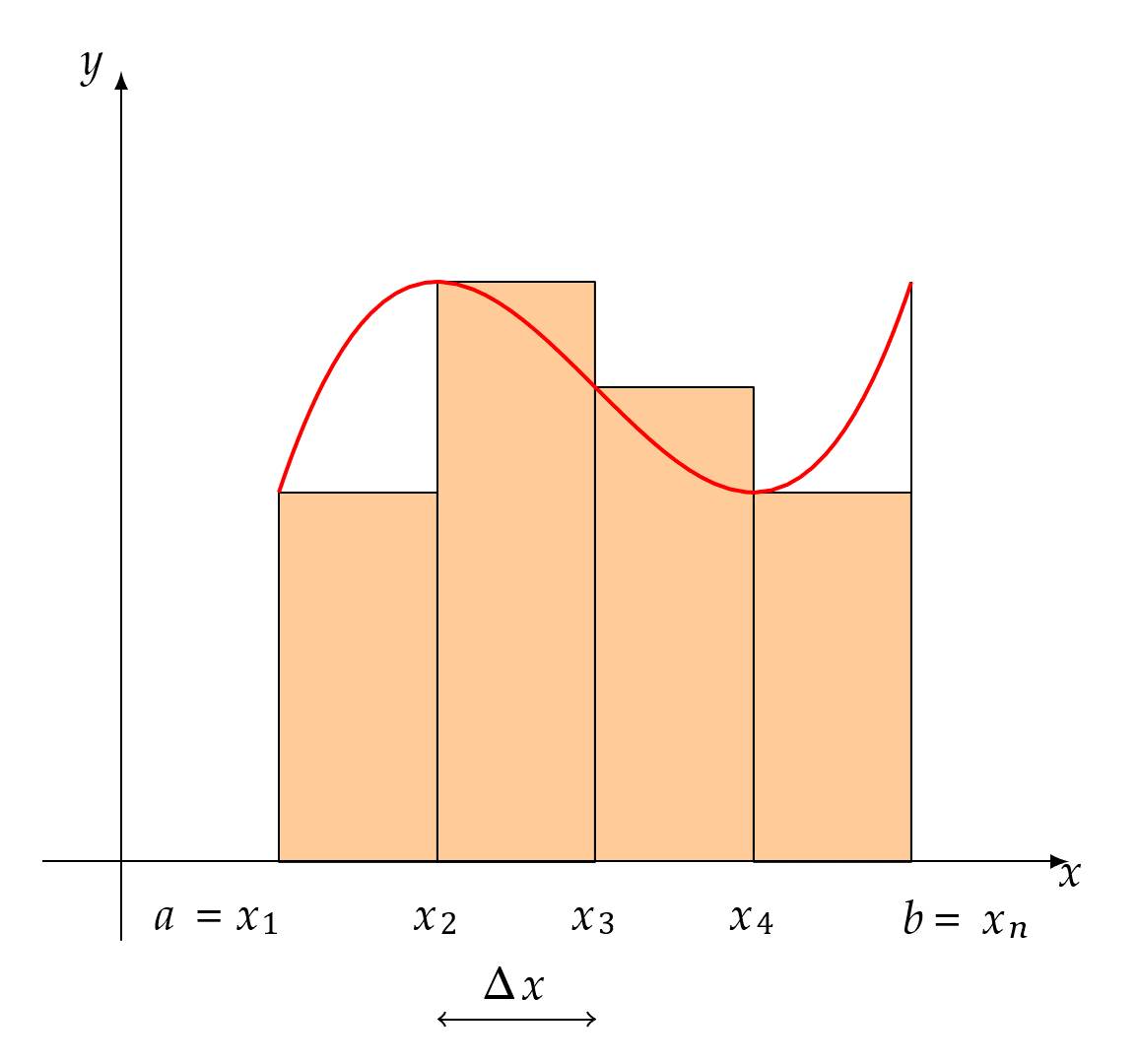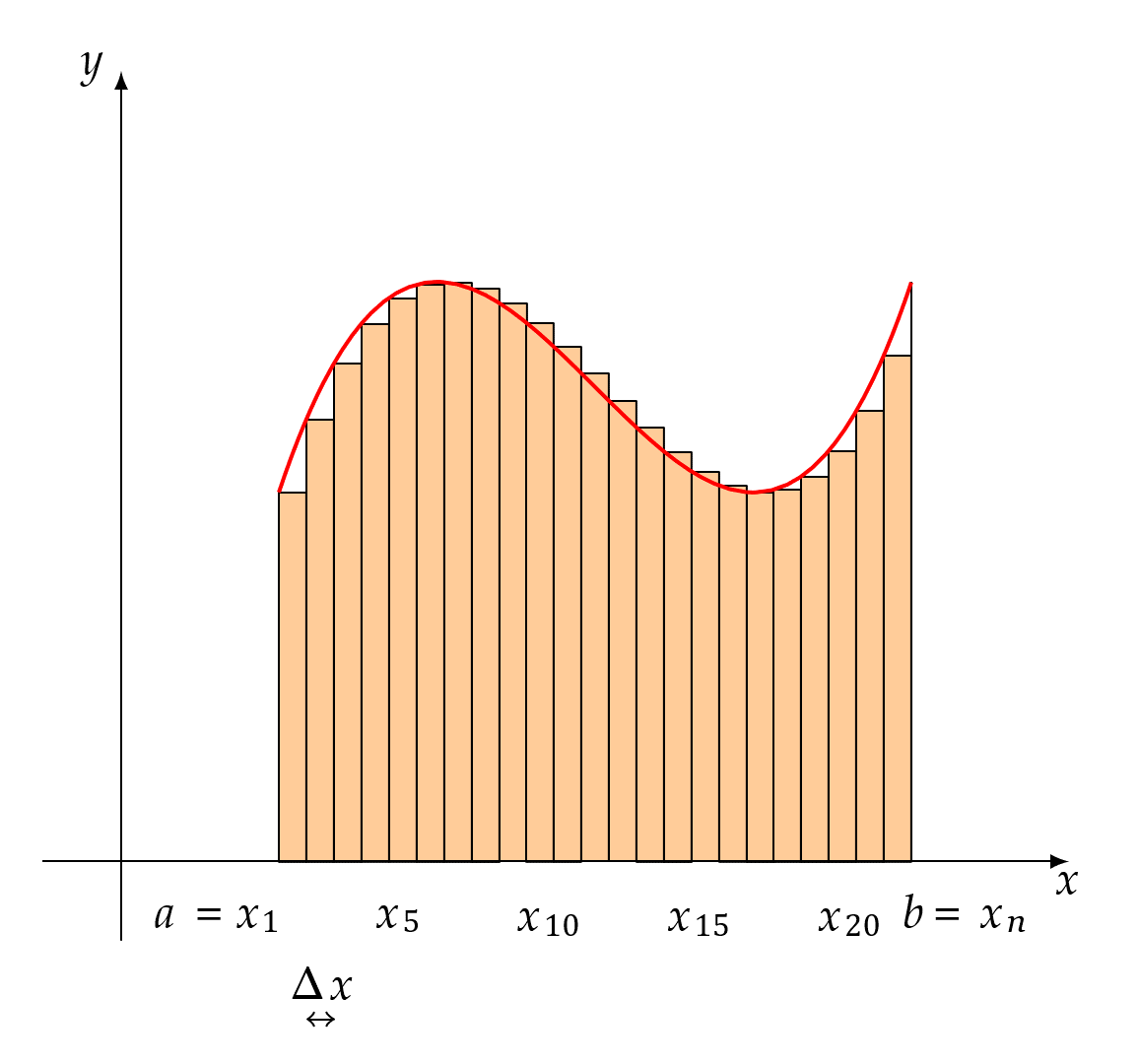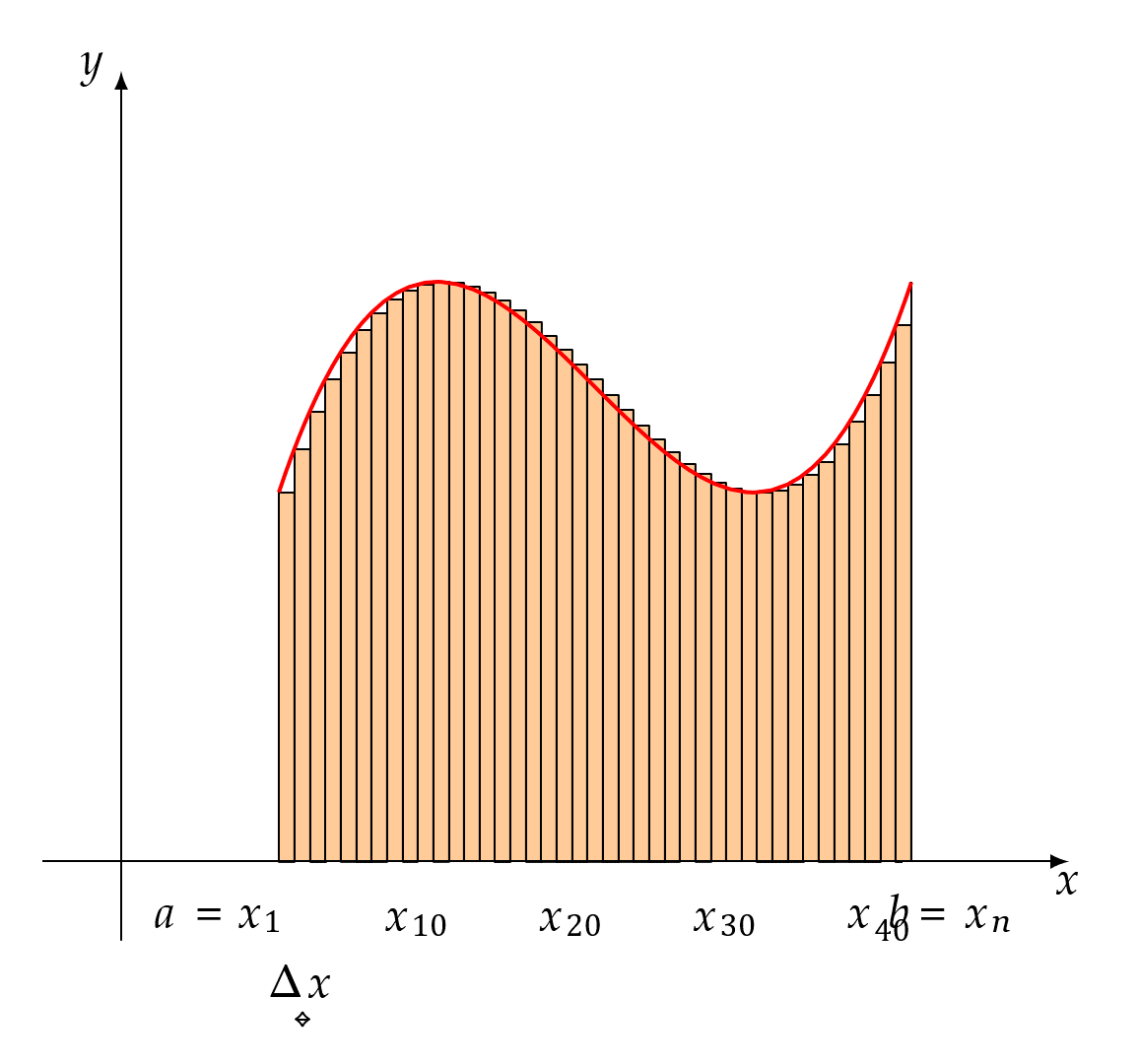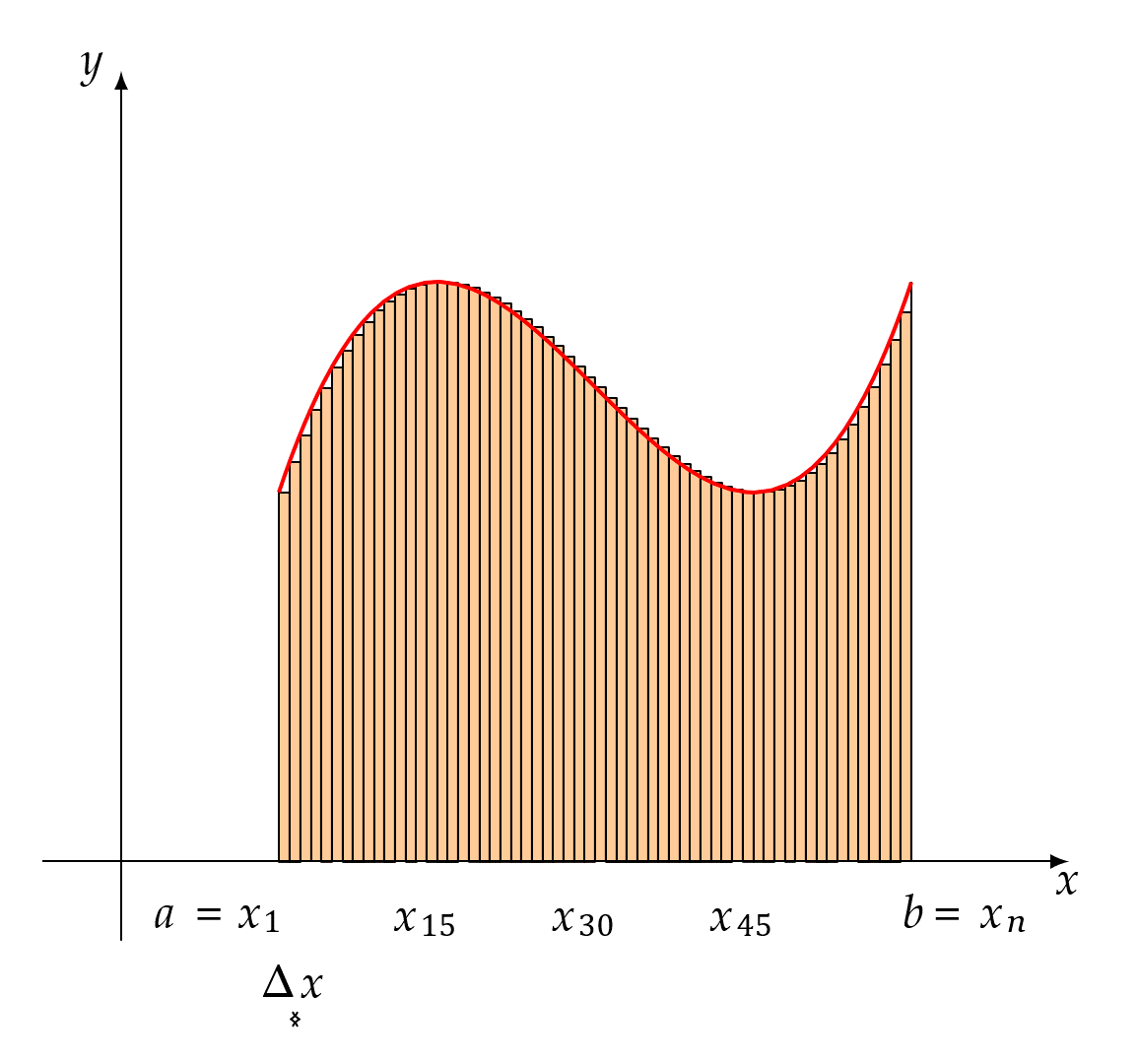
As the animated image shows, the sum of the areas of these rectangles becomes closer and closer to the curvilinear area as their bases become shorter and shorter. Although it is said that the limit represents the area of the curvilinear shape, one critical underlying question is whether the limit represents the exact value of the curvilinear area or just an approximation. The question arises no matter how narrow each rectangle becomes, there are nearly as many curvilinear triangles as the rectangles, and their areas are not included in the sum at each step, but they do contribute to the curvilinear area.

So, is the limit the exact value of the curvilinear area or just an approximation? This is the question this lecture will answer.

Before I give the final answer, I’d like to illustrate the answer with an example. Let’s calculate the area of the trapezoid.

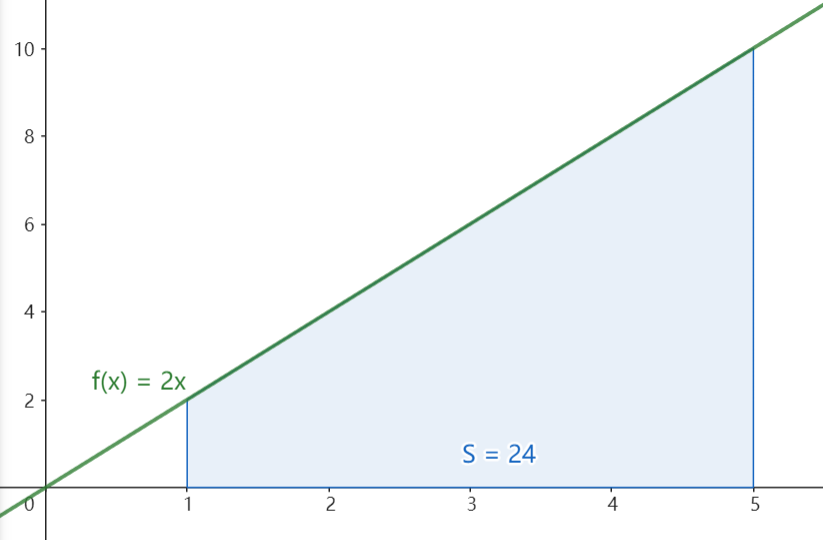
Since the area of a trapezoid is one half the altitude times the sum of the bases, so the area is $\frac{(2 + 10) \bullet 4}{2} = 24$ .

Similarly, the area can also be calculated using the calculus method. We break up the interval from 1 to 5 into n equal parts, each of width Δx.

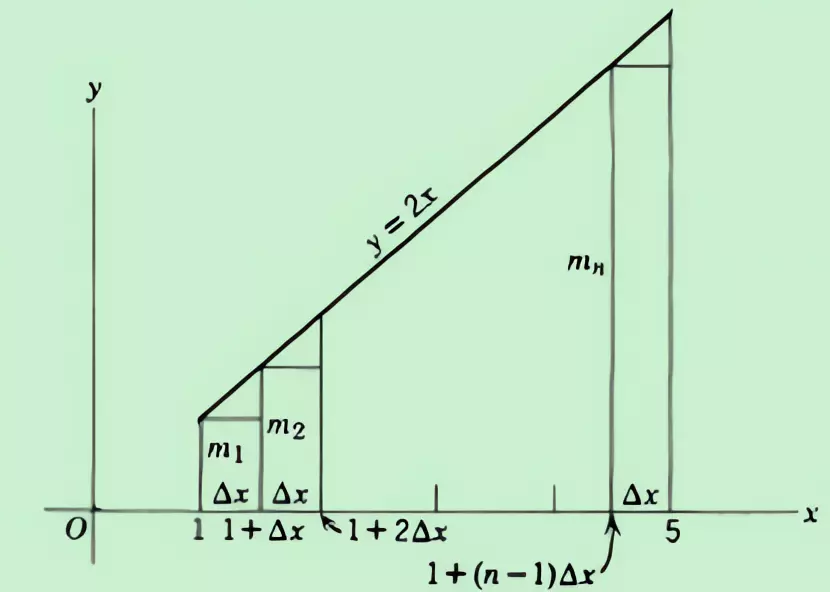
Sum the areas of these rectangles and then take the limit as the area of the trapezoid according to the calculus method:
$ $\begin{aligned} S_{n} &= 2\Delta x + 2(1 + \Delta x)\Delta x + 2(1 + 2\Delta x)\Delta x + \cdots + 2\lbrack 1 + (n - 1)\Delta x\rbrack\Delta x \\ &= 2\Delta x \cdot \frac{\lbrack 2 + (n - 1)\Delta x\rbrack \cdot n}{2} \\ &= n\Delta x\lbrack 2 + (n - 1)\Delta x\rbrack \\ &= 24 - \frac{16}{n} \end{aligned}$ $

we still get the answer 24, and we see that the area given by the calculus method agrees with the result obtained by the plane geometry. So the example suggests that the area calculated by the limit or calculus method is an exact value rather than an approximation, even though the areas of the curvilinear triangles are not summed into the total area at each step. But why is it an exact value rather than an approximation?

Let’s recall the calculus method to calculate the curvilinear area, the first step is to divide the shape into a lot of narrow rectangles, sum their areas, and then take the limit of the sum to be the value of the area as the rectangles become narrower and narrower. The limit method involves an infinite number of steps, during the process, although the existence of the curvilinear triangles, they become smaller and smaller as the number of the rectangles becomes more and more, and then we get better and better approximations to the area, most importantly, any approximation, no matter how precise, will be surpassed by a better one in the infinite process, in other words, any good approximation will be excluded in the infinite process, so what is left is only the actual value, this is the same idea as the method of exhaustion used by Archimedes to calculate the area of a circle.

All seemingly good approximations are excluded in the infinite process, what is only left is the actual value. The same idea applies to the principles of calculating the instantaneous speed, and the slope of the tangent.

In order to better understand the basic idea of the calculus or the limit method, I advocate using the phrase “the method of infinite exhaustion” instead of “limit” to aid understanding. The word “infinite” here emphasizes the infinite process within, it's the key to get the exact value.
This is it.